Crossing paths
When did you last cross paths with an old friend? With someone unexpected? Something about it feels impossible, you say it's a small world and catch up. How could it have ever happened? Is it really?
Simple world
We will have a simple model. The world will be a square of size . We have two people (you) and (someone unexpected). Each starting somewhere and following a path until it ends. The start and end points will be lattice points (integer coordinates). For example, is a lattice point but is not. What will happen to the probability of intersection as (the world) gets bigger?
Let's start by understanding the space of possibilities.
Number of Points
Let's start by counting the points on different sized grids
- points on a grid
- points on a grid
- points on a grid
- points on a grid
We will call this , the set of points
Defining a Path
From , we select- A starting point
- An ending point from the remaining points
- if is different from
- if is the same as
We will call this , the set of paths (line segments)
Path Pairs
For two people to cross paths, we need
- Your path selected from
- Someone unexpected's path selected from the remaining paths
This gives us possible path pairs. We call this , the set of path pairs
Size of Space
Let's see how quickly our space grows with grid size
- Points
- Grows proportional to
- Paths
- To make a path, we pick points from
- Grows proportional to ()
- Path pairs
- To make a pair, we pick lines from
- Grows proportional to ()
Intersection Probability
For every pair in , we check if intersects with and count it up=
| Grid Size | Probability | Runtime |
|---|---|---|
| 2 × 2 | 370/630 ≈ 0.587 | 0 secs |
| 6 × 6 | 222,624/690,900 ≈ 0.322 | 1.1 secs |
| 10 × 10 | 7,197,450/26,350,170 ≈ 0.273 | 45 secs |
| 14 × 14 | 81,149,616/317,507,400 ≈ 0.256 | 9 mins |
The number of possible line pairs is growing quite fast. The time it takes to check all the line pairs for intersection is also growing quite large. The probability is going down. Will and not cross paths? 😢
In the visualization above, we can see how the space of intersections looks. The bottom grid represents . The axes of the grid represents (all the lines). So the cell at represents picking the first line from , which is and picking the third line from , which is . So the grid represents picking every possible pair of lines and this is exactly what is. If the cell is white, then an intersection occurred. We won't count pairs where and are the same line - this is why the diagonal is all black.
What is a crossing?
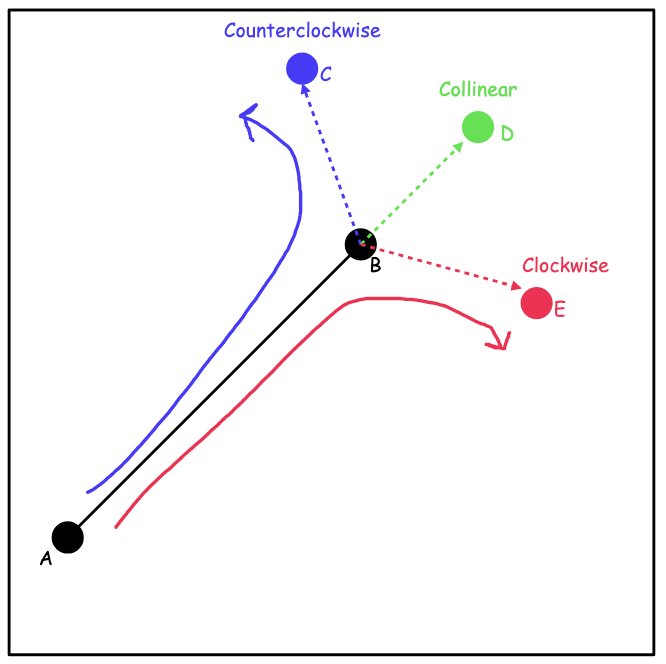
Your line has 2 points and . Take a
look at the first diagram. has a slope, . The point C is counterclockwise to because is greater than . The point D is collinear to because equals . The point E is clockwise to because is less than .
Think of it as riding a bike along the line and then turning towards the target point, C, D, or E. The way you turn
decides your orientation. We can use this to figure out if two lines intersect.
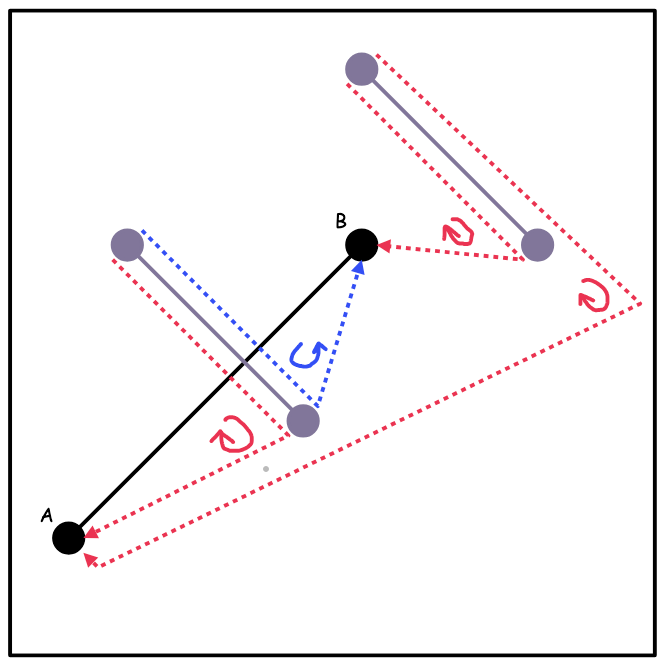
Take a look at the second diagram. When the gray line is not intersecting,
its orientation to point A is clockwise. Its orientation to point B is also
clockwise. Imagine the gray line is sliding down to the left. When it crosses
B, the orientation to B will become counterclockwise! This means and have to be on different sides of the gray line. Also, the gray points have
to be on different sides of .
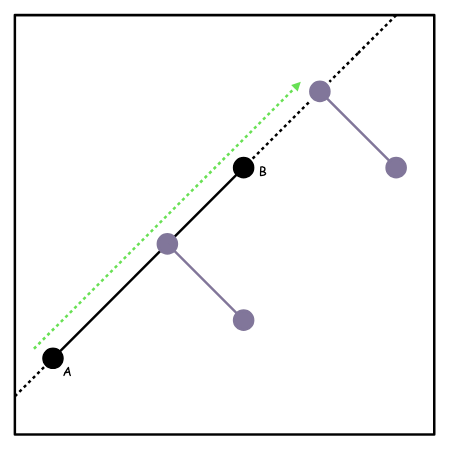
Take a look at the third diagram. If the point is collinear with , then we just need to check if the point is on the line segment.
3 Orientations: Clockwise, Counterclockwise, or Collinear
Notice the orientation changes when the gray segment actually intersects
Collinear
Approximate
There is a lot of path pairs to check for intersection and it would take way too much time to check them all as the grid gets very large. Let's cross paths with Stanisław Ulam, the inventor of the Monte Carlo method. Monte Carlo is a way to determine "something" by repeated sampling. In our case, "something" is the probability of intersection. Think of the game Red Light, Green Light from Squid Games or childhood.
When the large robot doll turns around, instead of making you less alive, she records your position. If she turns around twice, she has your location at 2 points in time. If we connect these 2 points, that might be a bad approximation of your running path. The more she turns around and records your location, the more accurately she can see your path.
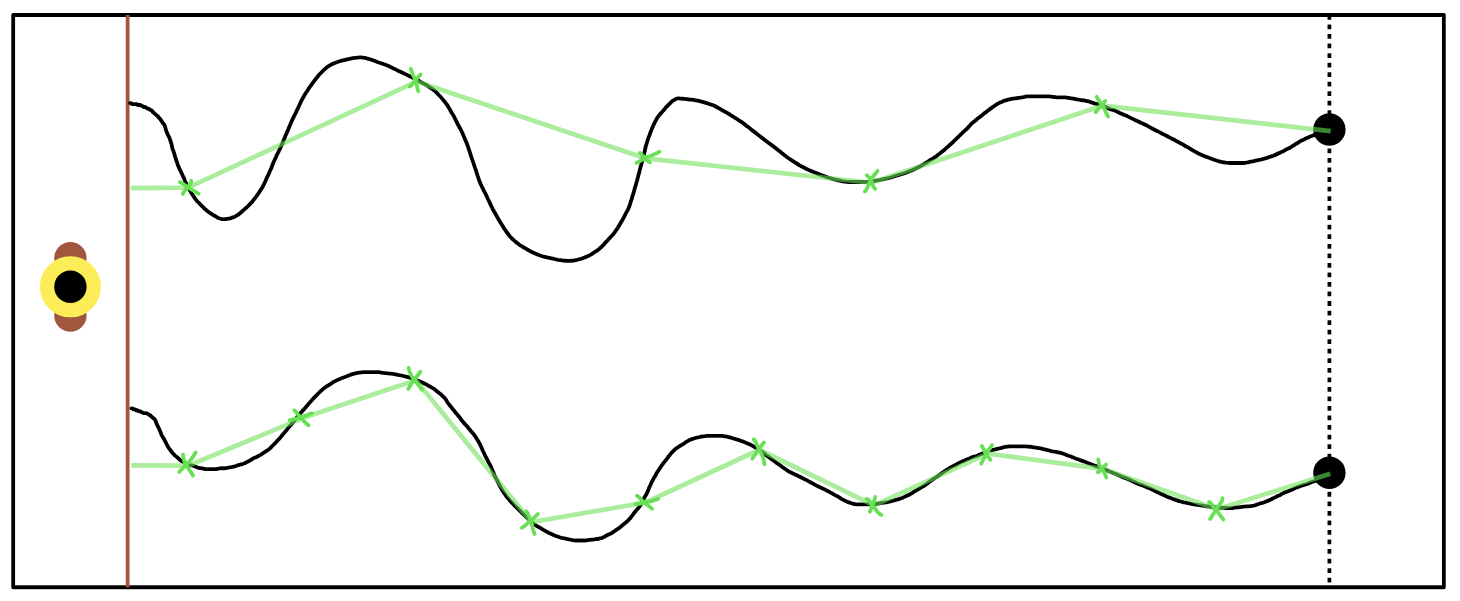
The approximate path gets closer to the actual path with more samples
We pick 2 paths at random and see if they intersect. Monte Carlo gets
close to the exact probability as we get more samples. As the grid size
increases, the space (number of path pairs) increases. To get a
reasonable "vibe" of the space, we should take a good amount of samples.
Otherwise, our approximation could be wrong.
As the grid gets big, it looks like the approximate probability is approaching
some value. What could it be 🤔
Polygons
Checking every possible path pair becomes impractical. At grid size 20, we will have 30 billion pairs to check! Monte Carlo only gives us approximations. Let's flip our perspective. When is it impossible for paths not to cross?
What happens when we extend your path to the boundaries of our grid world? This line naturally divides the space into two regions - the upper polygon (blue) and the lower polygon (orange). If someone unexpected starts their path from a point in the upper polygon, we can calculate a complementary region of points in the lower polygon. Play with the visualization below, you can see this as the yellow colored points. Creating a path from to any point in will guarantee an intersection! This will work no matter which polygon we pick a point from.
Polygon Method Steps
Instead of checking every possible path pair for intersection, we can:
- Take any possible path
- Extend the path to the grid boundaries and identify the two polygons
- Go through every point in one of the polygons
- Count how many points are in the complementary region of points
This method transforms our problem from finding actual intersections to finding guaranteed ones, making our calculations much more manageable for larger grids.
It's a small world
Now we can count all the ways in which paths are guaranteed to cross. But what happens to this number as our world grows larger and larger? Can the number of non-intersecting paths keep up with the growth of intersecting ones?
Growth of Possible Paths
First, let's understand how many possible paths exist:
- Each path needs four coordinates:
- Each coordinate can range from to
- Therefore, the number of possible line segments grows proportional to
Counting Intersections
Using the polygon method, we can count intersections:
- For a given path , we pick one of the polygons which has number of points proportional to
- For each point in , we have the number of valid intersection points in the complementary region which is proportional to
- The number of intersecting lines is proportional to (# of points in ) × (# of points in )
- This gives us (choosing the first line) × (intersecting lines)
- The total growth of intersections is proportional to
Why the World Stays Small
- Total possible path pairs grow proportional to
- Number of intersecting paths also grows proportional to
- Their ratio (the probability of intersection) approaches a non-zero constant
- Even as , there's still a significant chance of paths crossing!
We can also think about when paths definitely won't cross. We could calculate an average area of the lower and upper polygon. Picking two points from the same polygon would give us a non-intersecting line. The area of each region varies based on , but averaging across all possible line segments gives us a lower bound on the probability of non-intersection.
Even in an infinitely large world, the chance of crossing paths never disappears. It really is a small world after all ☺️
Further exploration
- Probability of intersection if we pick points on the surface of a sphere or cube?
- Is the probability in one space equal to probability in another space? For example, a rectangle and the surface of a cylinder
- What if your path is not a straight line?
Note
This problem might have an exact answer, feel free to look it up. I couldn't resist trying to work out such a simply stated problem.